Blog-- Thoughts on data analysis, software development and innovation management. Comments are welcome Post 51 Linear regression in Machine Learning16-Oct-2011Today is the deadline for submitting the first Review Questions of Stanford's Machine Learning course, which regard Linear Regression (LR) with one variable and Linear Algebra. I enrolled late this week and my experience with it has been very exciting. Andrew Ng has an outstanding ability to teach, and the lectures are most understandable with the digital board. But I'm a bit confused wrt the intended audience, because the gradient descent algorithm is presented along with the basic matrix operations (in a sense, the former is taught at 4th year of engineering while the latter at 1st year). Anyhow, the course seems great. Nevertheless, maybe I would prefer presenting certain topics as natural evolutions of evident problems, and provide alternative ways to solve a particular problem in order to avoid method idealisms. For example, after the LR problem is presented as an optimisation problem with respect to half the Mean Squared Error criterion, I would emphasise the general form of this cost function to ease the transition to other methods (e.g., the negative corpus log-likelihood for the Logistic Regression, to come on October 24th - 30th). Then, the solution of this optimisation problem could first be set in closed-form (by solving the null derivative equation). But in face of its apparent difficulty, numeric methods would then be well regarded. In this sense, the Gradient Descent (GD) is one possible solution, but others like the Nelder-Mead method or Genetic Algorithms could also work well. Finally, the batch GD algorithm is noted as a pitfall for speed, discussing a fancy learning rate and skimming over the stopping criterion. Hence, online GD algorithms like the sequentiality assumption of the Least Mean Square rule (aka Widrow-Hoff rule) or the random learning pattern of the Stochastic GD could be of help here. Although they sometimes lack a bit of accuracy because of the single-sample approximation (see the figure below), their use is a must for real-time processing environments.
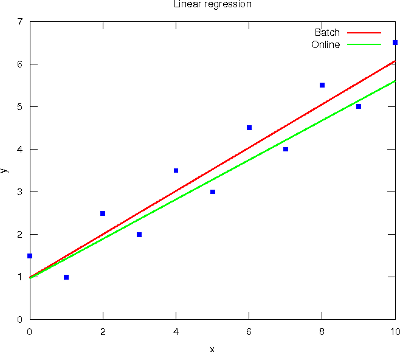 The Octave code used to generate the above regressions is available here for the batch version, and here for the online version. |
All contents © Alexandre Trilla 2008-2025 |