Blog-- Thoughts on data analysis, software development and innovation management. Comments are welcome Post 52 Logistic Regression in Machine Learning30-Oct-2011This week's work in the Stanford ml-class has covered Logistic Regression (LR) and Regularisation in regression models (both linear and logistic). I do believe Prof. Ng when he states that LR is the most widely used classification method in the world. A well-designed LR strategy is determined to pass any test with flying colours, hence its renown effectiveness. LR is full of wonders, most of which are grasped in the lecture, but I would still like to review a few aspects that I think deserve a deeper analysis. First of all, I find that the philosophy of learning of the LR is of most interest, and this is quite skimmed over in the lecture. Its discriminative strategy modelling the boundaries among the classes is shown, but maybe the contrast with its counterpart generative strategies (such as Naive Bayes) would have made it more understandable, like the classification lecture that Prof. Crammer gave at LxMLS. I'm keen on seeing the reverse of the coin (or some reasonable alternative) when learning (and teaching) something. In other research fields such as Natural Language Processing, LR is renamed to Maximum Entropy, supporting that the distribution of the learnt model is as uniform as possible (hence with maximum entropy) given that it does not assume anything beyond what is directly observed in the training data. Moreover, I have also found lacking the notice of its origin, which intended to symmetrically model the odds-ratio of a prediction, see this. With regard to the multiclass generalisation with the One-Versus-All strategy (as if it only was a dichotomic classifier like a Support Vector Machine, coming soon), I particularly missed the Multinomial distribution, which naturally integrates this multiclass requirement. In addition, it gives birth to the so called Multinomial Logistic Regression, generally used in Computational Linguistics software suites like LingPipe. What is more, their implementation is based on the Stochastic Gradient Descent algorithm (Carpenter, 2008), which is a randomised online interpretation of the classical gradient descent algorithm shown at ml-class. One thing I've enjoyed is the tackling of complex problems with LR. By complex I mean needing a hypothesis function more sophisticated than a typical linear discriminant. The fun has been in discovering the need of regularisation to prevent overfitting with such a new complex function (which comes at a price). And perhaps I would even have delved beyond the Tikhonov regularisation to unearth other methods like the Ridge Regression and the Lasso, i.e., LR with Gaussian and Laplace priors on the parameters, respectively. Finally, to see the behaviour of LR wrt the ideal boundary, let's follow what was done in the LxMLS lab for classification, see this guide. Let's conduct a very controlled and simple experiment with two equally sized instance groups coming from normal distributions representing the two classes. Since the true joint distributions P(X,Y) that generate the data are thus known, the Bayes Optimal decision boundary can be analytically calculated (Duda, et al., 2001). The simplest case occurs when the features are statistically independent and each feature has the same variance. Geometrically, this corresponds to the situation in which the instances fall in equal-size hyperspherical clusters, and the boundary hyperplane is the perpendicular bisector of the line linking the means of the clusters. The figure below shows the Bayes Optimal and the Decision Boundary obtained with LR superimposed on the scatter plot of the data instances. As it can be observed, LR is very close to the optimum boundary. Depending on the distributions that generate the data (usually unknown), these boundaries may differ more or less, but LR equally yields a highly effective solution.
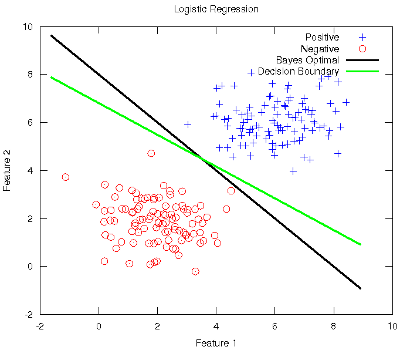 The Octave code used to generate the figure is available here. Note that the rest of the ml-class files need be present along with the former.
-- |
All contents © Alexandre Trilla 2008-2025 |