Alexandre Trilla, PhD - Data Scientist |

Blog

-- Thoughts on data analysis, software development and innovation management. Comments are welcome

Least Squares regression with outliers is tricky

23-Jul-2012

If reams of disorganised data is all you can see around you, a Least Squares regression may be a sensible tool to make some sense out of them (or at least to approximate them within a reasonable interval, making the analysis problem more tractable). Fitting functions to data is a pervasive issue in many aspects of data engineering. But since the devil is in the details, different objective criteria may cause the optimisation results to diverge considerably (especially if outliers are present), misleading the interpretation of the study, so this aspect cannot be taken carelessly.

For the sake of simplicity, linear regression is considered in this post. In the following lines, Ordinary Least Squares (OLS), aka Linear Least Squares, Total Least Squares (TLS) and Iteratively Reweighted Least Squares (IRWLS) are discussed to accurately regress some points following a linear function, but with an outlying nuisance, to evaluate the ability of each method to succeed against such a noisy instance (this is fairly usual in a real-world setting).

OLS is the most common and naive method to regress data. It is based on the minimisation of a squared distance objective function, which is the vertical residual between the measured values and their corresponding current predicted values. In some problems, though, instead of having measurement errors along one particular axis, the measured points have uncertainty in all directions, which is known as the errors-in-variables model. In this case, using TLS with mean subtraction (beware of heteroskedastic settings, which seem quite likely to appear with outliers; otherwise the process is not statistically optimal) could be a better choice because it minimises the sum of orthogonal squared distances to the regression line. Finally, IRWLS with a bisquare weighting function is regarded as a robust regression method to mitigate the influence of outliers, linking with M-estimation in robust statistics. The results are shown as follows:

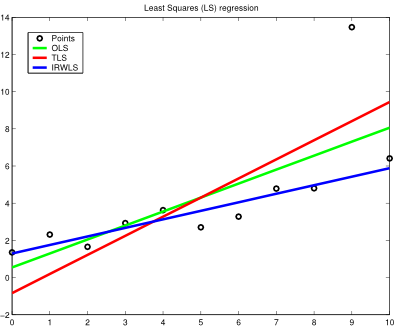According to the shown results, OLS and TLS (with mean subtraction) display a similar behaviour despite their differing optimisation criteria, which is slightly affected by the outlier (TLS is more affected than OLS). Instead, IRWLS with a bisquare weighting function maintains the overall spirit of the data distribution and pays little attention to the skewed information provided by the outlier. So, next time reliable regression results are needed, the bare bones of the regression method of use are of mandatory consideration.

Note: I used Matlab for this experiment (the code is available here). I still do support the use of open-source tools for educational purposes, as it is a most enriching experience to discover (and master) the traits and flaws of OSS and proprietary numerical computing platforms, but for once, I followed Joel Spolsky's 9th principle to better code: use the best tools money can buy.