Alexandre Trilla, PhD - Data Scientist |

Blog

-- Thoughts on data analysis, software development and innovation management. Comments are welcome

Perceptron learning with the overused Least Squares method

02-Nov-2012

Following Geoffrey Hinton's lectures on Neural Networks for Machine Learning, this post overviews the Perceptron, a single-layer artificial neural network that provides a lot of learning power, especially by tuning the strategy that is used for training the weights (note that Support Vector Machines are Perceptrons in the end). To keep things simple, 1) no regularisation issues will be covered here, and 2) the weight optimisation criterion will be the minimisation of the squared error cost function, which can be happily overused. In another post, the similarity between using the least squares method and the cross-entropy cost through the negative log-likelihood function (as it is reviewed in class) assuming a Gaussian error was already discussed. So using one or the other won't yield much effectiveness improvement for a classic toy dataset sampled from two Gaussian distributions.

Therefore, the ability of the perceptron to excel in classification tasks effectively relies on its activation function. In the lectures, the following functions are reviewed: binary, linear, logit and softmax. All of them provide their own singular learning capability, but the nature of the data for the problem at hand is always a determining factor to consider. The binary activation function is mainly used for describing the Perceptron rule, which updates the weights according to the steepest descent. Although this method is usually presented as an isolated golden rule, not linked with the gradient, the math is clearer than the wording:

Eq. a) corresponds to the update rule with a binary activation function, Eq. b) with a linear function and Eq. c) with a logit function.

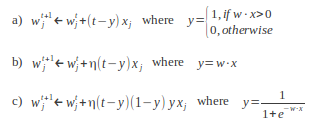The gradient for the logit is appended in the figure above to see how a different activation function (and thus a different cost function to minimise) provides an equivalent discriminant function (note that the softmax is a generalisation of the logit to multiple categories, so it makes little sense here):

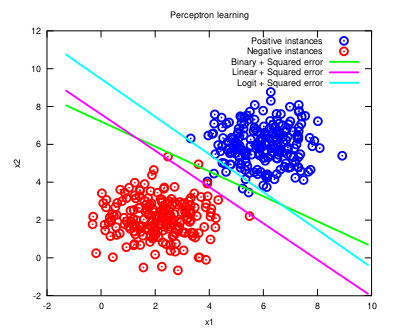As it can be observed in the plot, the form of the activation indeed shapes the decision function under the same cost criterion (not of much use here, though). In certain situations, this can make the difference between a good model and an astounding one. Note that different optimisation functions require different learning rates to reach convergence (you may check the code here). And this process can be further studied with many different activation functions (have a look at the variety of sigmoids that is available) as long as the cost function is well conformed (i.e., it is a convex function). Just for the record, the Perceptron as we know it is attributed to Rosenblatt, but similar discussions can be found with respect to the Adaline model, by Widrow and Hoff. Don't let fancy scientific digressions disguise such a useful machine learning model!